Questão 41 – Prova do Estado – (OFA) 2.014 – Professor de Educação Básica II

Os pares ordenados (0, 0) e (1, 3) pertencem ao gráfico de uma função polinomial do 2.º grau. O máximo dessa função tem abscissa x = 2. Logo, o valor da função no ponto de abscissa x = –1 é

(A) 5.

(B) 4.

(C) 0.

(D) –4.

(E) –5.

Solução: (E)

Aplicando o Método de Resolução de Problemas segundo Polya:

1° – Compreensão do Problema

Determinar a o valor de f (– 1) de uma função do segundo grau [f (x) = a · x² + b · x + c ] que possui os pontos P₁ = (0, 0) e P₂ = (1, 3).

Como a função apresenta um valor de máximo (a < 0) então a concavidade da parábola está voltada para baixo, logo f (x) = – a · x² + b · x + c.

Temos a abscissa do vértice da parábola: x_v = 2.

2° – Estabelecimento de um Plano

Utilizar os dados do enunciado para obter a função e calcular f (– 1).

                                             

3° – Execução do Plano

f (x) = – a · x² + b · x + c

Para o ponto P₁ = (0, 0), temos f (0) = 0:

0 = – a · 0² + b · 0 + c → c = 0

f (x) = – a · x² + b · x + c → f (x) = – a · x² + b · x + 0 → f (x) = – a · x² + b · x

Para o ponto P₂ = (1, 3), temos f (1) = 3:

3 = – a · 1² + b · 1 → – a + b = 3

Sabemos que no vértice da parábola: x_v = 2.

x_v = – b / [2 · (– a)] → 2 = – b / [2 · (– a)]  → – 4 · a + b = 0

Resolvendo o sistema de equações:

– a + b = 3

– 4 · a + b = 0

a = 1

b = 4

Então a função do enunciado se refere a f (x) = – x² + 4 · x. Calculando f (– 1).

f (– 1).= – (– 1).² + 4 · (– 1) = – 1 – 4 = – 5

4° – Avaliação

Questão envolvendo o estudo equação / função do segundo grau.

Outra forma de encontrar f (x) é observar que 0 é uma das raízes da função, visto que P₁ = (0, 0) → f (0) = 0.

Sendo x_v = 2 a abscissa do vértice então a outra raiz é 4, visto que pelo vértice passa uma linha perpendicular ao eixo das abscissas denominada eixo de simetria que divide a parábola em duas partes iguais.

As raízes da equação do segundo grau estão à mesma distância do eixo de simetria. A função f (x) = – a · x² + b · x + c tem como forma fatorada f (x) = – a · (x – x₁) · (x – x₂), sendo x₁ e x₂ raízes da função.

f (x) = – a · (x – x₁) · (x – x₂) → f (x) = – a · (x – 0) · (x – 4) → f (x) = – a · (x) · (x – 4)

Para o ponto P₂ = (1, 3), temos f (1) = 3:

3 = – a · (1) · (1 – 4) → 3 = – a · (1) · (– 3) → a = 1

f (x) = – 1 · (x) · (x – 4) → f (x) = (– x) · (x – 4)

f (– 1) = [– (– 1)] · [(– 1) – 4] = [1] · [– 5] = – 5

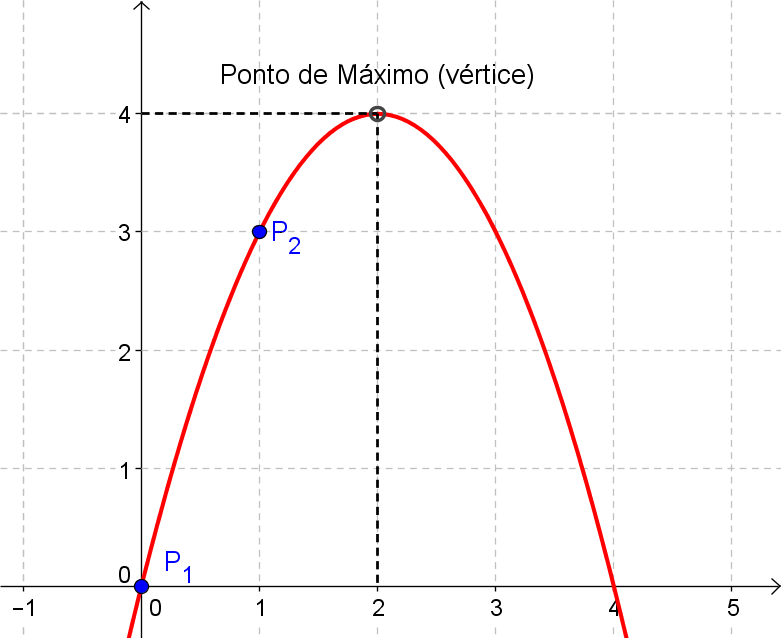Figura 1: Gráfico de f (x).