Dados os conjuntos
A = {x Є R : x2 < 1} e B = {x Є R : 1 / x < 2}
pode-se afirmar que
(A) A ∩ B = ]1/2 , 1[
(B) A ∩ B = ] –1 , 0[ È ]1/2 , 1[
(C) A ∩ B = ] –1 , 1/2[
(D) A ∪ B = ] –1 , 0[ È ]1/2 , +∞[
(E) A ∪ B = ] –∞ , 1/2[
Solução: (B)
Para resolver esta questão devemos realizar o estudo dos sinais de cada equação. Temos vários métodos para realizar este estudo. Utilizo comumente o método apresentado no livro "Introduccion al Calculo" de James Stewart.
Para a equação do conjunto “A”.
x2 < 1 → x2 – 1 < 0 (inequação do segundo grau)
Considerando x2 – 1 = 0, obtemos as raízes –1 e 1.
|
]–∞ , –1[
|
]–1 , 1[
|
]1 , +∞[
|
x2 – 1
|
+
|
–
|
+
|
Pelo estudo de sinal sabemos que o conjunto solução desta equação são os números que pertencem ao intervalo: ] –1 , 1[ .
Para a equação do conjunto “A”.
1 / x < 2 → 1 / x – 2 < 0 → (1 – 2 ∙ x) / x < 0 (inequação quociente)
Na inequação quociente devemos levar em consideração o fato de a incógnita estar no denominador, já que neste caso temos restrições na solução.
Resolvemos a equação do numerador e do denominador de forma separada:
Para o numerador:
1 – 2 ∙ x = 0 → x = 1 / 2
Para o denominador
Neste caso sendo o denominador apenas x temos uma restrição, pois o denominador pode ser qualquer número real diferente de 0, logo x ≠ 0.
|
]–∞ , 0[
|
]0 , 1/2[
|
]1/2 , +∞[
|
1 – 2 x
|
+
|
+
|
–
|
x
|
–
|
+
|
+
|
(1 – 2 x) / x
|
–
|
+
|
–
|
Pelo estudo de sinal sabemos que o conjunto solução desta equação são os números que pertencem ao intervalo: ] –∞ , 0[ ∪ ]1/2 , +∞[ .
Para chegar à conclusão final, temos que analisar o que ocorre com o sinal em ambas às equações em relação aos intervalos dados pelos números {-1, 0, 1/2, 1}:
|
]–∞ , –1[
|
]–1 , 0[
|
]0 , 1/2[
|
]1/2 , 1[
|
]1 , +∞[
|
x2 – 1
|
+
|
–
|
–
|
–
|
+
|
(1 – 2 x) / x
|
–
|
–
|
+
|
–
|
–
|
As alternativas se referem a união (∪) e a intersecção (∩) entre os conjuntos A e B.
A ∪ B são os intervalos que satisfazem qualquer um dos conjuntos, ou seja, são os intervalos no qual as equações geram resultados negativos, neste caso são todos os números reais exceto o 0. logo:
A ∪ B = R – {0}
A ∩ B são todos os resultados que satisfazem ambos os conjuntos, ou seja, são os intervalos no qual ambas as equações geram resultados negativos, neste caso são todos os intervalos que s exceto o 0, neste caso são os intervalos ]–1 , 0[ e ]1/2 , 1[ , logo:
A ∩ B = ]–1 , 0[ ∪ ]1/2 , 1[
A resolução poderia ser realizada graficamente. Na Figura 1, apresento os gráficos das equações.
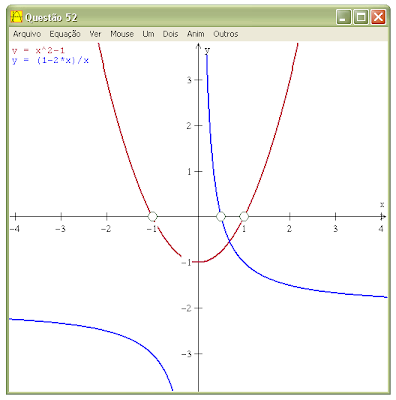 |
Figura 1: Gráfico das Equações do Conjunto A e do Conjunto B.
|
Pelo gráfico podemos determinar a solução do problema. Observe que temos que reorganizar ambas as equações obtendo para o conjunto A: x2 – 1 < 0, e para o conjunto B: (1 – 2 ∙ x) / x < 0, no conjunto B temos uma restrição por se tratar de um quociente, então x ≠ 0.
Como ambos os conjuntos são formados por números negativos e não nulos. Observamos os intervalos ]–1 , 0[ , ]0 , 1/2[ e ]1/2 , 1[ .
Somente entre os intervalos ]–1 , 0[ e ]1/2 , 1[ temos partes de ambos os gráficos, então são estes intervalos que satisfazem a condição de A ∩ B, explicado anteriormente.
Resolução a pedido da Profª. Ane.





Comentários