
CONSIDERE AS INFORMAÇÕES A SEGUIR PARA RESPONDER ÀS QUESTÕES 18, 19 E 20.
Os matemáticos gregos da Antiguidade, além da grande contribuição que deram à Geometria, também apontaram a não existência de um número racional que pudesse representar com exatidão a medida de muitos comprimentos.
Pitágoras e seus discípulos, por exemplo, situam-se entre os primeiros grupos de matemáticos que estudaram a necessidade de se descobrirem novos números além dos racionais. O famoso Teorema de Pitágoras proporcionou o reconhecimento desses números, que hoje chamamos de irracionais.
(Adaptado de: Matemática – Idéias e desafi os, Iracema e Dulce, Ed. Saraiva)
Questão 18
Aristóteles (384-322 a.C.) foi para Atenas estudar com Platão e, durante seus estudos, formulou a tese de que corpos de massas diferentes caem com tempos diferentes ao serem abandonados de uma mesma altura, sem qualquer tipo de verificação experimental.
Com o desenvolvimento da Ciência e o início do processo experimental por Galileu Galilei (1564-1642), realizou-se um experimento para comprovar a tese de Aristóteles. Galileu verificou que soltando dois corpos de massas diferentes, com volumes e formas iguais, simultaneamente, de uma mesma altura e de um mesmo local, ambos atingiram o solo no mesmo instante.
Com relação ao experimento realizado por Galileu, afirma-se que
I. a aceleração da gravidade foi considerada a mesma para ambos os corpos abandonados.
II. os corpos chegaram ao mesmo instante no solo, pois os pesos tornaram-se iguais.
III. a resistência do ar não influenciou no resultado obtido por Galileu.
Está correto o que se afirma em
(A) I, apenas.
(B) I e II, apenas.
(C) I e III, apenas.
(D) II e III, apenas.
(E) I, II e III.
Solução: (C)
I. a aceleração da gravidade foi considerada a mesma para ambos os corpos abandonados ↠ Correto.
II. os corpos chegaram ao mesmo instante no solo, pois os pesos tornaram-se iguais ↠ Incorreto.
III. a resistência do ar não influenciou no resultado obtido por Galileu ↠ Correto.
Quando Galileu estudou a queda de corpos, desconsiderou a resistência do ar, utilizando objetos com o mesmo formato.
Um corpo em queda livre próximo do superfície da Terra sofrem a influência da aceleração da gravidade, $g$. O cálculo da força da gravidade, $P$, expressa segundo a expressão $P=m \times g$, onde $m$ é a massa do corpo, mostra que a massa do copo não se altera durante o movimento.
No vácuo não importa o formato do objeto, sem a influência da resistência do ar, todos os objetos chegam no mesmo instante ao solo.
Questão 19
A partir dos sentidos, o homem começou a ter contato com o mundo físico que o cerca. O médico grego Galeno, no século II a.C., sugeriu que as sensações de quente e frio fossem medidas com base em uma escala de quatro divisões.
Após 1300 anos, Harme de Berna desenvolveu uma escala de temperatura baseada nas latitudes terrestres. Galileu, utilizando a expansão do ar, desenvolveu um termoscópio com uma escala mais precisa para leitura, dividida em graus de calor
Com o passar dos tempos e a aquisição de novos conhecimentos, desenvolveram-se termômetros que utilizavam diferentes substâncias - álcool, óleo de linhaça, mercúrio, gás - até os termômetros digitais, sempre acompanhados de diferentes escalas, com maior precisão de leitura, que foram padronizadas e aperfeiçoadas - ºC e ºF, por exemplo - até chegar a uma escala de referência, Kelvin (K), que possui o zero absoluto.
De acordo com o texto, o desenvolvimento do termômetro e das escalas
(A) facilitou a leitura da quantidade de energia transferida entre dois corpos.
(B) permitiu medir temperaturas mais baixas que o zero absoluto.
(C) permitiu que a indústria de construção de termômetros aperfeiçoasse as escalas.
(D) aconteceu pela necessidade de o homem comparar qual objeto estava quente ou frio.
(E) tornou difícil ao homem adquirir conhecimentos para aperfeiçoar a construção de escalas.
Solução: (D)
O principal motivo para o desenvolvimento do termômetro e das escalas termométrica é o de comparação entre os corpos.
O fato determinação a temperatura não garante a leitura da quantidade de energia, desta forma a alternativa (A) está incorreta. O zero absoluto é a temperatura hipotética, no qual cessa o movimento do átomo, não existindo temperatura abaixo do zero absoluto, que é igual a 0 K (zero Kelvin), logo a alternativa (B) está incorreta.
O aperfeiçoamento dos termômetros não ocorreu pela industria, mas estudos realizados pelos físicos e cientistas, logo a alternativa (C) está incorreta. Com os estudos e experimentos realizados com os termômetros primitivos e com utilização de diversas substâncias permitiu a evolução da termologia e a formulação das escalas termométricas.
Questão 20
Considere um quadrado com $3\sqrt{2} \; cm$ de lado, inscrito em um círculo como mostra a figura.

O raio desse círculo mede, em centímetros
(A) $2$.
(B) $\sqrt{3}$.
(C) $\frac{3\sqrt{3}}{2}$.
(D) $3$.
(E) $2\sqrt{3}$.
Solução: (D)
A Figura 1 mostra o resultado da análise do enunciado
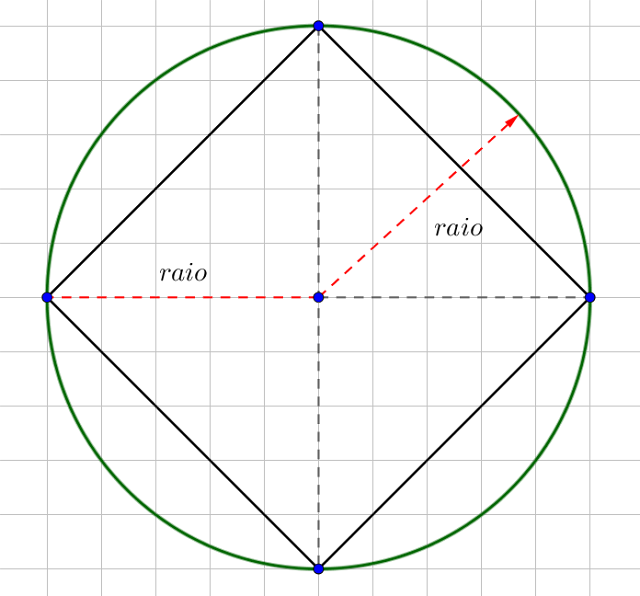 |
| Figura 1: Análise do enunciado mostra que o raio tem medida igual a metade da diagonal do quadrado. |
Observe que a podemos obter a medida do diâmetro da circunferência, calculando a diagonal do quadrado (vide Figura 2).
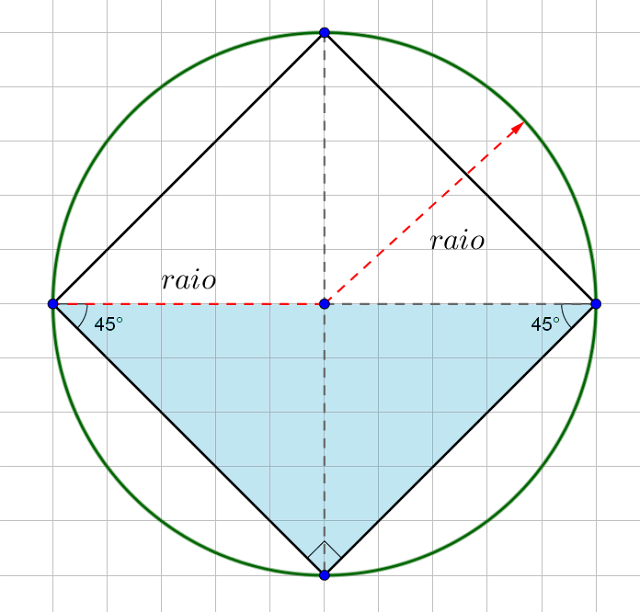 |
| Figura 2: Indicação que a diagonal do quadro pode ser obtido mediante o calculo da hipotenusa do triângulo indicado. |
Podemos observar que temos um triângulo retângulo, onde a hipotenusa é igual ao diâmetro, o os lados do quadrado são os catetos. Aplicando o Teorema de Pitágoras:
$h^{2}=c^{2}+c^{2}$
$h^{2}=\left ( 3\sqrt{2} \right )^{2}+\left ( 3\sqrt{2} \right )^{2}=2\cdot \left ( 3\sqrt{2} \right )^{2}=2\cdot 3^{2} \cdot \left (\sqrt{2} \right )^{2}=2\cdot 9 \cdot 2=36$
$h^{2}=36 \Rightarrow h=\sqrt{36}=6\; cm$
Se o diâmetro mede 6 cm, então o raio mede metade do diâmetro $raio=\frac{6 \; cm}{2}=3 \; cm$.

Não se esqueça que a matemática está em todo lugar! Aprecie!










Comentários