 Considere a charge a seguir como referência para responder Às questões de 7 a 16.
Considere a charge a seguir como referência para responder Às questões de 7 a 16.
(BROWNE, Dik. O melhor de HAGAR, O HORRÍVEL. Porto Alegre. L&PM, 2005. L&PM POCKET.)
Questão 08
A dedicação de Eratóstenes aos estudos forneceu-lhe conhecimentos para determinar a esfericidade da Terra, e ele obteve um resultado satisfatório, diante dos equipamentos e materiais a que tinha acesso.
Imagine que Hamlet, filho de Hagar, pensasse em comprovar a esfericidade da Terra utilizando observações astronômicas, alguns conceitos de ótica e a sombra da Terra.
Nessas condições, Hamlet faria uso de seus conhecimentos referentes
(A) ao eclipse solar.
(B) ao eclipse estelar.
(C) ao eclipse lunar.
(D) à rotação da Lua.
(E) à rotação da galáxia.
Solução: (C)
Quando observamos um eclipse lunar em que o Sol projeta a sombra da Terra na Lua, podemos notar que a borda da sombra é arredondada, desde o início até o final no eclipse (vide Figura 8.1).
 |
| Figura 8.1: Visualização da sombra da Terra projetada na Lua durante um eclipse. |
| Referência de Estudo |
| Disciplina |
Série / Ano |
Bimestre |
| Ciências |
| Conteúdo: Terra e Universo – Nosso planeta e sua vizinhança cósmica. |
|
7ª / 8° |
3° |
| Fonte:São Paulo (Estado) Secretaria da Educação. Currículo do Estado de São Paulo: Ciências da Natureza e suas tecnologias / Secretaria da Educação; coordenação geral, Maria Inês Fini; coordenação de área, Luis Carlos de Menezes. – São Paulo : SEE, 2010. |
Fonte:
University Lowbrow Astronomers: Lunar Eclipse Photographs [Image 10] -
http://umich.edu/~lowbrows/astrophotos/lunar-eclipse/moon10.html. Acessado em 21 de novembro de 2.016.
Questão 10
Para Hagar, a Terra tem a forma de um cubo, porém, na realidade, pode-se considerá-la uma esfera de raio $R$.
Sabendo-se que o volume de uma esfera de raio $R$ é dado por $\frac{4}{3} \pi R^{3}$ e imaginando-se que a Terra cúbica de Hagar tenha o mesmo volume da Terra real, então a aresta desse cubo, escrita em função de $R$, é igual a
(A) $\left ( \sqrt[3]{\frac{4}{3} \pi} \right ) \cdot R$.
(B) $\sqrt[3]{\frac{4}{3} \pi R}$.
(C) $\left ( \frac{\sqrt[3]{4 \pi}}{3} \right )\cdot R$.
(D) $\frac{2}{3} \pi R$.
(E) $\frac{4}{3} \pi R$.
Solução: (A)
Segundo o enunciado devemos considerar o volume da Terra esférica, $V_{\mathrm{Terra \; Esf\acute{e}rica}}$, igual ao volume da Terra cúbica, $V_{\mathrm{Terra \; C\acute{u}bica}}$:
| $V_{\mathrm{Terra \; Esf\acute{e}rica}} = V_{\mathrm{Terra \; C\acute{u}bica}}$ |
01 |
O volume de um cubo é obtido segundo a expressão: $V_{\mathrm{Cubo}}$=\mathrm{aresta}^{3}$, logo
| $V_{\mathrm{Terra \; C\acute{u}bica}}=\mathrm{aresta}^{3}$ |
02 |
Segundo o enunciado:
| $V_{\mathrm{Terra \; Esf\acute{e}rica}} = \frac{4}{3} \pi R^{3}$ |
03 |
Substituindo a Equação (2) e a Equação (3) na Equação (1), temos:
| $\frac{4}{3} \pi R^{3}= \mathrm{aresta}^{3}$ |
04 |
Para determinar a aresta desse cubo, escrita em função de $R$, devemos isolar a variável $\mathrm{aresta}$ na Equação (4):
$\frac{4}{3} \pi R^{3}= \mathrm{aresta}^{3} \Rightarrow \mathrm{aresta}^{3}=\frac{4}{3} \pi R^{3}$
$\sqrt[3]{\mathrm{aresta}^{3}}=\sqrt[3]{\frac{4}{3} \pi R^{3}}$
$\mathrm{aresta}=\sqrt[3]{\frac{4}{3} \pi R^{3}}$
| Referência de Estudo |
| Disciplina |
Série / Ano |
Bimestre |
| Matemática |
| Conteúdo: Geometria: Poliedros. |
|
6ª / 7° |
2° |
| Matemática |
| Conteúdo: Números: Álgebra. |
|
6ª / 7° |
4° |
| Matemática |
| Conteúdo: Geometria: Geometria: Volume do Prisma. |
|
7ª / 8° |
4° |
| Fonte:São Paulo (Estado) Secretaria da Educação. Currículo do Estado de São Paulo: Matemática e suas tecnologias / Secretaria da Educação; coordenação geral, Maria Inês Fini; coordenação de área, Nilson José Machado. – 1. ed. atual. – São Paulo : SE, 2011. |
Questão 11
A Lei de Gravitação Universal, proposta por Isaac Newton, permite dizer que a força de atração entre duas massas diminui conforme aumenta a distância entre elas. Sendo mais preciso, quando aumenta a distância entre seus centros de massa. Dependendo da geometria do corpo, o centro de massa coincide com o centro geométrico.
Considerando o mundo cúbico de Hagar, inclinado exatamente como o mostrado na tirinha, a força de atração entre a massa desse mundo e a massa do navio terá maior intensidade quando o navio estiver situado
(A) na face inferior do cubo.
(B) em qualquer aresta do cubo.
(C) em qualquer vértice do cubo.
(D) no ponto médio da face superior do cubo.
(E) apenas nos pontos médios das arestas do cubo.
Solução: (D)
Considerando a Lei de Gravitação Universal quanto mais próximos os centros de massa maior é a força de gravidade e considerando o centro de massa coincidindo com o centro geométrico então o navio fica mais próximo do centro do cubo, quando está no centro de uma das faces, ou seja, no ponto médio da face superior do cubo.
Analisando a Figura 11.1, podemos observar que dos três pontos em destaque (pontos em azul) o que está mais próximo do centro (ponto em vermelho) é aquele localizado no centro da face.
 |
| Figura 11.1: Construção geométrica para auxiliar a resolução. |
| Referência de Estudo |
| Disciplina |
Série / Ano |
Bimestre |
| Matemática |
| Conteúdo: Geometria: Poliedros. |
|
6ª / 7° |
2° |
| Fonte:São Paulo (Estado) Secretaria da Educação. Currículo do Estado de São Paulo: Matemática e suas tecnologias / Secretaria da Educação; coordenação geral, Maria Inês Fini; coordenação de área, Nilson José Machado. – 1. ed. atual. – São Paulo : SE, 2011. |
Questão 12
Acredita-se que observações realizadas pelos gregos são as primeiras evidências de que certo tipo de pedra, o ímã natural, atraía pedaços de ferro. Essas pedras eram encontradas na região de Magnésia, situada no litoral mediterrâneo, e sempre que se aproximavam pedaços de ferro a essas pedras, uma força magnética atuava no sentido de atraí-los.
Imagine que os tripulantes que navegam com Hagar o aconselhassem a não se aproximar da costa desse litoral com a embarcação, afirmando que estas pedras, esses ímãs naturais
I. poderiam desmontar o navio, retirando os pregos.
II. iriam atrair as moedas de ouro dos baús.
III. iriam desorientar a bússola.
As afirmações válidas dos tripulantes estão em
(A) I, apenas.
(B) II, apenas.
(C) I e II, apenas.
(D) I e III, apenas.
(E) I, II e III.
Solução: (D)
Segundo o enunciado o imã natural atrai o ferro então poderiam atrair os pregos de ferro do navio, causando o naufrágio. Da mesma forma poderia ocorrer uma desorientação da bússola que é de ferro.
| Referência de Estudo |
| Disciplina |
Série / Ano |
Bimestre |
| Ciências |
| Conteúdo: Ciência e tecnologia. |
|
5ª / 6° |
2° |
| Ciências |
| Conteúdo: Terra e Universo – Olhando para o céu. |
|
6ª / 7° |
1° |
| Ciências |
| Conteúdo: Ciência e tecnologia – Constituição, interações e transformações dos materiais. |
|
8ª / 9° |
1° |
| Fonte:São Paulo (Estado) Secretaria da Educação. Currículo do Estado de São Paulo: Ciências da Natureza e suas tecnologias / Secretaria da Educação; coordenação geral, Maria Inês Fini; coordenação de área, Luis Carlos de Menezes. – São Paulo : SEE, 2010. |
Questão 15
Imaginando-se que o barco de Hagar desloque-se por um mar, onde a densidade da água é constante em qualquer ponto, pode-se afirmar que a força de empuxo que age no navio
(A) diminui com o aumento da carga transportada.
(B) diminui com a diminuição da carga transportada.
(C) aumenta com a diminuição de carga transportada.
(D) aumenta o espaço percorrido devido ao aumento de velocidade média.
(E) diminui a velocidade média, provocando uma diminuição no espaço percorrido.
Solução: (B)
Empuxo é a força de reação que permite objetos flutuarem, então quando se diminui a carga do navio é necessário um menor empuxo para manter o navio flutuando.
| Referência de Estudo |
| Disciplina |
Série / Ano |
Bimestre |
| Ciências |
| Conteúdo: Ciência e tecnologia – Constituição, interações e transformações dos materiais. |
|
8ª / 9° |
1° |
| Fonte:São Paulo (Estado) Secretaria da Educação. Currículo do Estado de São Paulo: Ciências da Natureza e suas tecnologias / Secretaria da Educação; coordenação geral, Maria Inês Fini; coordenação de área, Luis Carlos de Menezes. – São Paulo : SEE, 2010. |
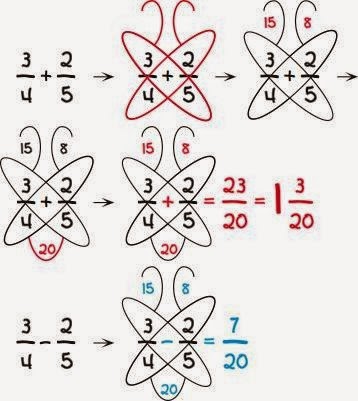
Não se esqueça que a matemática está em todo lugar! Aprecie!









Comentários