Um grande círculo azul escuro no meio do mar turquesa do Caribe atrai mergulhadores e turistas do mundo todo para Belize, na América Central.
O Great Blue Hole (Grande Buraco Azul) é uma caverna submersa com estalactites cercadas de animais marinhos de várias espécies, como arraias, peixes-papagaios e peixes-borboletas.
Localizado no Atol de Recifes Lighthouse, a cerca de 50 milhas a leste de Belize, o buraco é um círculo quase perfeito de cerca de 300 metros de diâmetro e 125 metros de profundidade, podendo ser visto inclusive do espaço.
(g1.globo.com/turismo-e-viagem/noticia/2012/12/grande-buraco-azul-no-meio-do-mar-e-paraiso-do-mergulhono-caribe.html Acesso em: 23.08.2013. Adaptado)
 |
| Great Blue Hole (Foto: U.S. Geological Survey) |
A circunferência da figura é uma representação esquemática do Grande Buraco Azul em que:
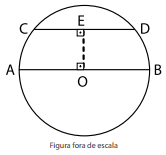
- o ponto O é o centro da circunferência;
- o segmento AB é um diâmetro da circunferência;
- os pontos C e D pertencem à circunferência;
- as retas AB e CD são paralelas;
- o ponto E pertence à corda CD; e
- as retas AB e OE e são perpendiculares.
Nessas condições, admitindo-se que a medida da corda seja 240 m, então a medida do segmento será, em metros,
(A) 93.
(B) 90.
(C) 87.
(D) 84.
(E) 81.
Fonte: http://www.vestibulinhoetec.com.br/provas-gabaritos/
Solução: (Anulada)
Aplicando o Método de Resolução de Problemas segundo Polya:
1° – Compreensão do Problema
É uma pena terem se esquecido de definir qual segmento deveria ser calculado, entretanto tudo indica que seja o segmento OE. A questão é bem interessante.
Corda é o nome dado a qualquer segmento de reta que se inicia e se finda na circunferência.
Na figura se construirmos o segmento OC e o segmento OD, temos o triângulo CDO. Um fato interessante é que o ponto C pertence a circunferência, então o segmento OC tem medida igual ao raio desta circunferência. O mesmo fato ocorre com o ponto D (vide Figura 1).
 |
| Figura 1: Análise dos dados do enunciado. |
Portanto o segmento OC e o segmento OD são congruentes (iguais). O triângulo que apresenta medidas de lados iguais é chamado de triângulo isóscele.
O segmento OE é perpendicular a corda CD, portanto, pelas características do triângulo isóscele, o segmento OE é a altura do triângulo CDO, sendo que o ponto E é o ponto médio da corda CD.
2° – Estabelecimento de um Plano
Termos então que calcular a altura do triângulo isóscele CDO. Para isto consideramos o triângulo retângulo CEO, reto no ponto E (vide Figura 2).
 |
| Figura 2: Triângulo retângulo CEO, reto no ponto E. |
Para calcular o segmento OE (um dos catetos) utilizamos o Teorema de Pitágoras, sendo a medida do segmento CE (um dos cateto) igual a 120 metros e a medida do segmento OC (a hipotenusa) igual a 150 metros.
3° – Execução do Plano
Determinando a medida do segmento OE:
OC2
= CE2 + OE2
OE2
= OC2 – CE2
OE = √ ( OC2 – CE2
) = √ ( 1502 – 1202 ) = √ ( 22500 – 14400 ) =
= √8100
Fatorando 8100 para determinar a raiz quadrada:
8100
4050
2025
675
225
75
25
5
|
2 (unidade=0 divisível por 2)
2 (unidade=0 divisível por 2)
3 (2+0+2+5=9 divisível por 3)
3 (6+7+5=18→1+8=9 divisível por 3)
3 (2+2+5=9 divisível por 3)
3 (7+5=12→1+2=3 divisível por 3)
5 (unidade=5 divisível por 5)
5 (unidade=5 divisível por 5)
|
1
|
|
Portanto 8100 = 22 · 34 · 52
√8100 = √(22·34·52) =√22 · √34 · √52 = 2 · 32
· 5 = 90 metros
4° – Avaliação
Para a resolução desta questão é necessário um conhecimento sobre conceito de geometria e de desenho geométrico. Infelizmente um erro causou a anulação.






Comentários
Parabens pelo blog, ajuda muitas pessoas
Adorei
Beijos
kworldofbooks.blogspot.com.br
por favor, me explique porque a hipotenusa é de 150 m.
Grata!
Noeli
A hipotenusa é 150 m pelo fato do diâmetro do buraco é de 300 m .. logo o raio é de 150 m ...
Sds